Abstract

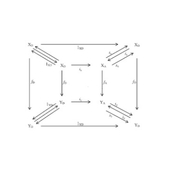
Our conscious experiences are qualitative and unitary. The qualitative universals given in particular experiences, i.e. qualia, combine into the seamless unity of our conscious experience. The problematics of quality and cohesion are not unique to consciousness studies. In mathematics, the study of qualities (e.g., shape) resulting from quantitative variations in cohesive spaces led to the axiomatization of cohesion and quality. Using the mathematical definition of quality, herein we model qualia space as a categorical product of qualities. Thus modeled qualia space is a codomain space wherein composite qualities (e.g. shape AND color) of conscious experiences can be valued. As part of characterizing the qualia space, we provide a detailed exemplification of the mathematics of quality and cohesion in terms of the categories of idempotents and reflexive graphs. More specifically, with qualities as commutative triangles formed of cohesion-preserving functors, first we calculate the product of commutative triangles. Next, we explicitly show that the category of idempotents is a quality type. Lastly, as part of showing that the category of reflexive graphs is cohesive, we characterize the adjointness between functors relating cohesive graphs to discrete sets. In conclusion, our category theoretic construction of qualia space is a formalization of the binding of qualitative features (colors and shapes) into the cohesive objects (colored-shapes) of conscious experiences. Compared to the feature-vector accounts of conscious experiences, our product-of-qualities account of consciousness is a substantial theoretical advance.