Abstract

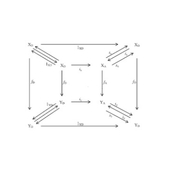
Notions such as śūnyatā, catuṣkoṭi, and Indra's net, which figure prominently in Buddhist philosophy, are difficult to readily accommodate within our ordinary thinking about everyday objects. Famous Buddhist scholar Nāgārjuna considered two levels of reality: one called conventional reality, and the other ultimate reality. Within this framework, śūnyatā refers to the claim that at the ultimate level objects are devoid of essence or "intrinsic properties", but are interdependent by virtue of their relations to other objects. Catuṣkoṭi refers to the claim that four truth values, including contradiction, are admissible in reasoning. Indra's net refers to the claim that every part of a whole is reflective of the whole. Here we present category theoretic constructions that are reminiscent of these Buddhist concepts. The universal mapping property definition of mathematical objects, wherein objects of a universe of discourse are defined not in terms of their content, but in terms of their relations to all objects of the universe is reminiscent of śūnyatā. The objective logic of perception, with perception modeled as [a category of] two sequential processes (sensation followed by interpretation), and with its truth value object of four truth values, is reminiscent of the Buddhist logic of catuṣkoṭi. The category of categories, wherein every category has a subcategory of sets with zero structure within which every category can be modeled, is reminiscent of Indra's net. Our thorough elaboration of the parallels between Buddhist philosophy and category theory can facilitate better understanding of Buddhist philosophy, and bring out the broader philosophical import of category theory beyond mathematics.